Раствор конуса потерь. Критические питч-углы.

Рис. 1. Схема движения частицы в магнитном поле. Определения параметров.
Представим себе частицу, захваченную в магнитном поле Земли (Рис. 1). Она, как хорошо известно, вращается вокруг силовой линии по ларморовскому кружку, совершает колебания вдоль силовой линии и испытывает азимутальный дрейф по всем долготам вокруг Земли. Периоды этих движений увеличиваются в порядке перечисления.
Рассмотрим частицу у вершины силовой линии (точка с напряженностью поля B0 в правой части рисунка). Пусть она находится на оболочке с параметром L (измеряется в радиусах земли Rз и равен расстоянию от центра Земли до вершины силовой линии). Если ее питч-угол 90°, она не испытывает колебаний и находится все время на одном и том же расстоянии от Земли (поле предполагается дипольным). Если же питч-угол меньше 90°, она начинает колебаться вдоль силовой линии и отражается в некоторой точке с напряженностью Bm (m - mirror, зеркальная точка, англ.). Пусть магнитная широта этой точки отражения равна λ, высота над Землей h. Чем меньше питч-угол на экваторе α, тем ниже высота точки отражения, тем меньше h.
Если так случилось, что в точке отражения частица заходит на высоту h меньше или порядка 100 километров, она может "погибнуть" в атмосфере и перестать участвовать в колебательном движении. Рассчитаем, каким должен быть питч-угол частицы на экваторе, чтобы точка отражения частицы располагалась на высоте h. Назовем этот питч-угол критическим (αкр). Частица с питч-углом меньше αкр погибнет заведомо, поэтому диапазон питч-углов от 0 до αкр называется конусом потерь, а αкр еще называется раствором конуса потерь.
Из закона сохранения первого адиабатического инварианта
 .
.
Уравнение силовой линии магнитного диполя
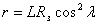 ,
,
напряженность магнитного поля в зависимости от r,λ
имеет вид
 .
.
где M~0,3 Гс - напряженность магнитного поля на экваторе Земли при L=1.
Значит, в точке у вершины силовой линии расстояние равно
 ,
,
а напряженность магнитного поля будет равна
 .
.
В точке отражения, исходя из тех же формул,
 .
.
Объединяя все упомянутые выше выражения, получаем для критического угла выражение вида
 .
.Осталась одна неизвестная величина λ, которую можно
рассчитать по уже использовавшейся формуле
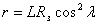 ,
,
где r в точке отражения равно Rз+h, значит
 .
.
Подставляя это выражение в формулу для критического угла, получаем

Перейдем от выражений типа Rз+h к выражениям, содержащим h/Rз. Получаем

Отсюда видно, что полученное выражение безразмерно и, скорее всего, ошибок в вычислениях не было.

Рис. 2. Зависимость критического питч-угла в градусах от L.
Если взять для расчета Rз=6400 км, h=100 км, диапазон по L от 1.02 до 7, получим следующую таблицу критических питч-углов:
|
L |
sin2α |
α, rad |
α ° |
|
1,02 |
0,99 |
1,46 |
83,51 |
|
1,03 |
0,96 |
1,37 |
78,36 |
|
1,04 |
0,93 |
1,31 |
74,98 |
|
1,06 |
0,88 |
1,22 |
70,09 |
|
1,08 |
0,84 |
1,16 |
66,42 |
|
1,1 |
0,8 |
1,11 |
63,43 |
|
1,2 |
0,64 |
0,93 |
53,38 |
|
1,3 |
0,54 |
0,82 |
47,10 |
|
1,4 |
0,46 |
0,74 |
42,56 |
|
1,5 |
0,40 |
0,68 |
39,06 |
|
2 |
0,23 |
0,5 |
28,65 |
|
3 |
0,11 |
0,34 |
19,74 |
|
4 |
0,07 |
0,27 |
15,46 |
|
5 |
0,05 |
0,22 |
12,88 |
|
6 |
0,04 |
0,19 |
11,13 |
|
7 |
0,03 |
0,17 |
9,85 |
Для меньших L получается значение  больше
единицы, и потому для них невозможно рассчитать соответствующие
критические питч-углы.
больше
единицы, и потому для них невозможно рассчитать соответствующие
критические питч-углы.
На Рис. 2 показана зависимость критического питч-угла от L. Подведем итоги:
- Частица с питч-углом, равным критическому или больше, попадает в конус потерь и гибнет в атмосфере.
- В максимуме радиационного пояса критический питч-угол порядка 10-20°. Чем ближе к Земле, тем шире раствор конуса потерь.
- Предельное значение раствора конуса потерь достигается на L<1.02.
Подчеркнем недостатки проведенного выше расчета и возможные пути их решения.
- Магнитное поле Земли на самом деле не дипольное. В литературе описаны методы модификации расчета, например, введением смещения центра диполя от центра Земли. Можно проводить расчет с помощью моделей магнитного поля (например, IGRF, модели Цыганенко и др.), которые гораздо ближе к реальному.
- Радиус Земли взят с большим округлением.
- Высота атмосферы не может быть определена в точности и 100 км это лишь приблизительная оценка.
Использованная литература
Х. Редерер, Динамика радиации, захваченной геомагнитным полем.
Мир, Москва, 1972.