Силовые линии точечного магнитного диполя.
Найдем уравнение силовой линии для точечного магнитного диполя (см. Рис), который расположен в начале координат и вектор которого направлен на юг (противоположно оси Z). Координаты в данной задаче будем использовать сферические.

Воспользуемся дифференциальным уравнением для силовой линии векторного поля общего вида:
 .
.
Учитывая, что  и
и  , можно записать, что
, можно записать, что
 .
.
Для магнитного диполя компоненты вектора поля равны:
 .
.
Подставляя их в уравнение, находим, что
 .
.
Где использовано начальное условие, что на экваторе (где магнитная широта равна нулю) расстояние до силовой линии равно r0. Подставляя явный вид компонент магнитного поля диполя, получаем уравнение
 ,
,
которое после простых преобразований приводится к виду
 .
.
Интегрируем его, используя начальное условие.
 .
.
Получаем
 .
.
Вычисляем подстановки
 .
.
Значит
 .
.
Экспоненцируя обе части выражения, получаем
 .
.
Или
 .
.
Введем параметр L, который характеризует расстояние до силовой линии на экваторе, выразив его в радиусах Земли (параметр Мак-Илвайна).
 .
.
Тогда уравнение для силовой линии точечного магнитного диполя принимает вид
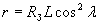 .
.